This study provides a pooled estimate of the distribution of incubation periods which may be used in subsequent modelling studies or to inform decision-making.
Several studies used data that were publicly available, therefore there is potential that some of the data may be used for more than one study.
This estimate will need to be revisited as subsequent data become available. Accordingly, we present an R Shiny app to allow the meta-analysis to be updated with new estimates.
Reliable estimates of the incubation period are important for decision-making around the control of infectious diseases in human populations. Knowledge of the incubation period can be used directly to inform decision-making around infectious disease control. For example, the maximum incubation period can be used to inform the duration of quarantine, or active monitoring periods of people who have been at high risk of exposure. Estimates of the duration of the incubation period, coupled with estimates of the latent period, serial interval or generation times, may help infer the duration of the presymptomatic infectious period, which is important in understanding both the transmission of infection and opportunities for control.1 Finally, decision-making in the midst of a pandemic often relies on predicted events, such as daily number of new infections, from mathematical models. Such models depend on key input parameters relevant to the transmission of the specific infectious disease. It is important that input parameters into such models are as robust as possible. Given that some models fit data to many parameters, only some of which are specifically of interest but all of which are interdependent, output estimates may be compared with the robust estimates as part of the validation of the model.
Earlier work has shown that for models of respiratory infections, statements regarding incubation periods are often poorly referenced, inconsistent or based on limited data.2 To date, many COVID-19 models have used input values from a single study. The decision on which study to use may vary from model to model. Recently, a systematic review of the epidemiological characteristics of COVID-19 reported that estimates of the central tendency of the incubation period ranged from 4 to 6 days.3 However, to the authors’ knowledge, no studies have yet sought to estimate the incubation period through a meta-analysis of data available to date. Furthermore, it is important to note that incubation periods are expected to vary across individuals within the population. For this reason, it is critically important to understand the variation in incubation periods (ie, the distribution) within the population. However, a single measure of central tendency (ie, mean or median) cannot adequately represent this variation.4 To address this, studies often fit mathematical distributions to incubation period data.
We hypothesised that a pooled estimate of the distribution of incubation periods could be obtained through a meta-analysis of data published to date. Therefore, the aim of this study was to conduct a rapid systematic review and meta-analysis of estimates of the incubation periods of COVID-19, defined as the period of time (in days) from virus exposure to the onset of symptoms. Specifically, we aimed to find a pooled estimate for the parameters of an appropriate distribution that could be subsequently used as an input in modelling studies and that might help quantify uncertainty around the key percentiles of the distribution as an aid to decision-making.
For the purpose of this study we followed the Meta-analysis of Observational Studies in Epidemiology guidelines.5 The outcome was defined as the time in days from the point of exposure (in this case, infection) to the onset of clinical signs; all observational studies were included in the analysis. Finally, the population was confirmed infected individuals, where an exposure time could be ascertained with some degree of certainty and precision.
It was not appropriate or possible to involve patients or the public in the design, or conduct, or reporting, or dissemination plans of our research.
A survey of the literature between 1 December 2019 and 8 April 2020 for all countries was implemented using the following search strategy. Publications on the electronic databases PubMed, Google Scholar, Embase, Cochrane Library as well as the preprint servers MedRxiv and BioRxiv were searched with the following keywords: ‘Novel coronavirus’ OR ‘SARS-CoV-2’ OR ‘2019-nCoV’ OR ‘COVID-19’ AND ‘incubation period’ OR ‘incubation’ (online supplementary table S1). The dynamic curated PubMed database ‘LitCovid’ was also monitored, in addition to national and international government reports. No restrictions on language or publication status were imposed so long as an English abstract was available. Articles were evaluated for data relating to the aim of this review, and all relevant publications were considered for possible inclusion. Bibliographies within these publications were also searched for additional resources. The initial searches were carried out by three of the investigators (ÁC, KH, FB). Authors of studies were contacted only to clarify reporting queries.
Results of searches were screened in two stages. First, titles and abstracts were screened, and only relevant articles retained. Studies were removed if they dealt with specific cohorts of cases that did not reflect the overall population. Next, articles were read in detail, studies were selected for meta-analysis if they reported either the parameters and CIs of the distributions fit to the data, or sufficient information to facilitate calculation of those values. Specifically, this included studies that reported: the point estimate and CIs or SEs of each parameter; the mean and SD on the original (non-transformed) scale with CIs; the mean and one or more percentiles of the distribution (with CIs); or two or more percentiles of the distribution (with CIs). Studies were excluded if they described the distribution (eg, with mean, median, percentile) but did not report any uncertainty around that figure. The selection of studies to include in the meta-analysis was conducted by the primary author (CM).
Once studies were shortlisted, two authors (CM, SJM) independently conducted appraisals of study quality. To the authors’ knowledge, no quality assessment tools are available to appraise studies reporting the incubation period of infectious disease. We used the Newcastle-Ottawa Scale for assessing the quality of non-randomised studies in meta-analyses6 as a basis and modified it according to important quality and reporting indicators for studies investigating incubation period. In particular, fields were added which assessed the accuracy and precision with which the exposure windows were defined. Fields relevant to non-exposed cohorts were removed. Finally, we replaced the ‘star’ system with a lettered categorical system for each item on the scale. The modified scale is provided as online supplementary material. After both authors had appraised the studies, the results were compared and differences in scores resolved through discussion until a consensus was reached.
On initial appraisal, it was apparent that the majority of studies fitted a lognormal distribution to the data. Earlier work has shown that this distribution is appropriate for many acute infectious diseases.2 7 Therefore, the study proceeded as the meta-analysis (pooled estimate) of the parameters of this distribution.
A variable (X) has a lognormal distribution when the log-transformed values follow a normal distribution with mean, mu, and variance, sigma2, that is:
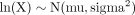
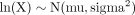
Methods exist for the meta-analysis of studies that combine a mix of log-transformed and non-transformed data.8 In this case we opted to transform data, where possible to the log-transformed scale, and obtain a pooled estimate of both mu and sigma.
Where the values for each parameter (mu and sigma) were available from the studies, along with corresponding CIs/SEs, these were extracted as reported. In the remaining studies, the values were calculated where possible from the information presented.
The mu and sigma parameters of the original lognormal distribution were calculated as:
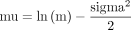
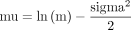


where v=variance (=SD2), and m=the mean of the distribution on the original (ie, non-log transformed) scale.
Similarly, upper and lower CIs of mu and sigma were found by substituting the upper and lower bounds of the mean or SD (from the original scale) into the equation above, one at a time, while holding the value for the other parameter constant (as the point estimate for that parameter).
Where studies reported the results as the mean and 95th percentile on the original scale, the ‘lognorm’ package in R was used to calculate the original values of mu and sigma and corresponding SEs or CIs.9
For studies reporting CIs, the SE was calculated as (upper bound – lower bound)/(2×1.96). Finally, for studies reporting the parameters relative to a referent value, the SE was calculated as:
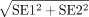
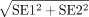
where SE1 and SE2 are the SEs of the estimate of the referent category and coefficient, respectively.
A random effects meta-analysis was conducted in RStudio V.1.2.5033,10 using the ‘metafor’ package,11 of the mu and sigma parameters of the lognormal distribution, specifying the point estimate and the SE using ‘yi’ (ie, the point estimate) and ‘sei’ (ie, the SE) arguments. Forest plots were produced using the same package. Quantitative estimates of bias were obtained using the Egger’s test and funnel plots. Heterogeneity was quantified using the I2 statistic and investigated by conducting subgroup analyses of the data set.
The mean and SD of the pooled estimate were converted to the original (ie, non-log transformed) scale as:
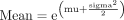
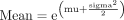


The upper and lower CIs were found by substituting, one at a time, the upper and lower bounds for mu and sigma and recalculating the subsequent figures for mean and SD.
The resulting distribution was plotted using the ‘ggplot2’ package in R.12 In addition, the distributions for studies that did not fit a lognormal distribution, but that reported the parameters of an alternative distribution fitted were also plotted alongside the pooled lognormal distribution.
Finally, an R Shiny app was created which allows the meta-analysis estimates to be updated as new data become available.
After initial search and selection of relevant papers and removing duplicates, 24 studies were available for appraisal.
Two papers were removed as they dealt with specific cohorts of cases—young adults13 and children.14
One study was removed since only the abstract was in English and there was not enough detail to extract the relevant results.15
Several papers were removed since they contained insufficient data or method description to facilitate their inclusion:
One study was removed since there was not enough detail in the paper to determine whether new parameters were being estimated or whether the parameters quoted were input values for their model.16
Seven papers were removed since the data were largely descriptive, with no CIs reported.17–23
One study was removed because the error terms associated with the mean, median and percentiles were not reported and there was not enough information presented to recover the parameters of the lognormal distribution.24
One study was removed25 since a novel statistical approach was employed that likely resulted in a significantly higher incubation period estimate to other studies.
Of the shortlisted studies (n=11), six reported lognormal distributions as best fitting the data.26–31 Of the remaining four, one reported that several distributions were trialled but it was not clear which distribution was used for the final estimates.32 However, these authors provided raw data which we used to fit the parameters of the lognormal distribution using the ‘rriskDistributions’ package.33 The remaining four studies reported that either Weibull or gamma distributions fitted the data better. Of these, two study also presented the results of a lognormal distribution fit to the data,34 35 facilitating their inclusion in the subsequent analysis. One of these studies35 reported the incubation period for two distinct cohorts: travellers and non-travellers to Hubei. The estimates for the cohorts were significantly different. The author suggested that this difference was possibly explained by multiple exposures in the traveller cohort. Therefore, we chose to only use the estimates reported for the non-traveller cohort in our analysis.
The final two studies reporting a Weibull36 and a gamma distribution37 were removed from further analysis at this stage, however, those distributions were plotted over the final distribution to evaluate the impact of removing those estimates. The characteristics of the final studies as well as the final mu and sigma values used for meta-analysis are shown in table 1.
Study size and extracted data for the lognormal mu and sigma parameters from the nine studies that were used for meta-analysis
Quality assessment (online supplementary table S2) indicated that few studies precisely outlined the exposure windows and symptom-onset windows that were used in their studies. Several studies reported that they conducted analysis on a small cohort of well-characterised cases. Likely this only includes individuals with short (1 day) exposure and symptom-onset windows. However, this was not clearly reported in several studies.
The initial pooled estimate of mu from this data set (ie, data set 1, n=8 studies) was 1.66 (1.55, 1.76) and the pooled estimate of sigma was 0.48 (0.42, 0.54). The I2 values were 75% and 56% for mu and sigma, respectively. Egger’s tests for mu and sigma were not statistically significant; p=0.31 and p=0.20 for mu and sigma, respectively. However, evaluation of the funnel plots (online supplementary figures S1 and S2) suggests the potential for bias associated with one of the studies included in the analysis.30 Evaluation of the meta-analyses results for mu demonstrated that two studies were responsible for much of the heterogeneity in the analysis of this value. In particular, the values reported by Ma et al30 and Backer et al34 were higher than the estimates from other studies. Both studies were further evaluated to determine whether these differences may have been due to methodological differences. The Backer et al34 study was subsequently excluded since it appeared that the exposure window was somewhat imprecisely defined which would have biased this estimate upwards. Conversely, the study reported by Ma et al30 used only patients where the exposure window was 3 days or less, with the majority of those of a 1 day duration. The meta-analysis was repeated with the Backer et al34 study removed (ie, data set 2, n=7 studies). The resulting pooled estimates were 1.63 (1.51, 1.75) and 0.50 (0.46, 0.55), while the I2 values were 75% and 24% for mu and sigma, respectively. Figures 1 and 2 show the resulting forest plots for the meta-analyses of mu and sigma, respectively, from data set 2 (n=8), that is, the nine studies from which the parameters were extracted, minus the Backer et al34 estimate.
Forest plot of the random effects (RE) meta-analysis of mu parameter of the lognormal distribution of incubation period.
Forest plot of the random effects (RE) meta-analysis of sigma parameter of the lognormal distribution.
Figure 3 shows the resulting density plot of the pooled distribution. Figure 4 shows the cumulative density function plot of the same (pooled distribution). In this instance, all possible combinations of distributions across the 95% CIs of the estimates of each of the mu and sigma values are plotted on the same graph. Table 2 shows the percentiles and corresponding CIs of the pooled lognormal distribution.
Probability density function of the pooled lognormal distribution of reported incubation period with mu=1.63 and sigma=0.50.
Cumulative distribution function of pooled lognormal distribution. Each possible combination of values between the 95% CIs of mu and sigma is plotted as single black lines.
Percentiles of the pooled lognormal distribution after simulating all possible combinations of mu and sigma within the 95% CIs of the pooled estimates of both parameters
Figure 5 shows the cumulative density function plots of the pooled lognormal distribution along with the estimates from the original studies. Finally, figure 6 shows the probability density function of the pooled lognormal distribution, plotted alongside the two studies that could not be included in the final meta-analysis due to the fact that they fit alternative distributions to the data.
Cumulative distribution function of pooled lognormal distribution for incubation period and original input studies.
For the purpose of this study we defined incubation period as the time in days from the point of COVID-19 exposure to the onset of symptoms. Online supplementary figure S3 shows a schematic of this time period with respect to other key parameters influencing COVID-19 transmission. Studies to determine incubation period are likely most precise during the early phase of the outbreak, before the pathogen is widespread.26 During this early phase, exposure windows can be determined with some confidence. Most studies achieved this by conducting the analysis based on travellers from an epicentre of infection (Wuhan) to another country/region that was free from infection at that time point or in the very early stages of the outbreak.
By definition, the required case data for the determination of individual incubation periods need to include both exposure (window) and onset of symptoms. Precisely estimating these events can be difficult. Symptom onset is based on case recall, whereas exposure is determined either from: movement history, thereby providing a window prior to movement of potential exposure, or a known window of exposure (from earliest to latest) to a confirmed case (close contact). However, exposure and/or symptom onset are rarely observed exactly. The methods used to deal with this include restricting the analysis to data from patients where the exposure window could be narrowed to a short window (eg, <3 days); taking a median point from the exposure window to determine the exposure time point. Alternatively, Linton et al29 included left exposure dates as parameters to be fitted in the model. However, several studies did not report the duration of the exposure and symptom-onset windows for cases used in their analyses. In many cases, these were described as ‘well characterized’ cohorts of cases and likely only included 1 day windows, however, we recommend that future studies explicitly report if this is the case.
After the initial meta-analysis we decided to remove the Backer et al34 study from the pooled estimate. The estimates from that study were found to be shifted considerably to the right compared with other estimates. Examination of that study identified that many of the patients had long exposure windows which would be expected to bias the estimate upwards. Interestingly, that study conducted an additional subset analysis of patients whose exposure windows were well defined and for these data, the mean incubation period dropped from 6.4 to 4.5 days. However, it is interesting to note that Ma et al30 restricted their analysis to patients with a 3-day exposure window and still found a mean incubation period of 7.4 days. Since this study had the largest sample size (n=587), it has a significant impact on the estimation of the lognormal parameters. Repeating the meta-analysis with both the Backer et al34 and Ma et al30 studies removed results in values of 1.58 (1.51, 1.64) and 0.47 (0.42, 0.53), respectively. With both of these studies removed the I2 values drop to 0% for both parameters. The corresponding mean and median are 5.48 and 4.85 days, respectively. Interestingly, removing this study also increases the precision of the estimate of the value for mu.
One of the weaknesses of our approach is that we extracted and analysed the parameters of the lognormal distribution independently. However, in reality the parameters and the initial distribution that they are fitted to are linked. We were unable to include two studies that did not fit lognormal distributions to the data. However, figure 6 demonstrates that the impact of removing these studies is likely to be small since they are similar to the pooled estimate, with one falling to the left of the pooled estimate, and the other falling to the right. Ideally, we would have fit distributions to the raw data available from each of the studies, in a way that facilitated the distributions to vary across studies. Such an approach was taken by Lessler et al2 in reviewing acute respiratory viral infections. However, the raw data were not available in all cases for the studies that we examined. Another limitation is that many of the papers included in this study used publicly available data to estimate incubation period. Therefore, there is a reasonable chance that several of the analyses have reused at least some of the same data. In these cases, the studies would not be independent of each other. Finally, since this study was conducted as a rapid review, we did not seek raw data from studies that were excluded, nor did we seek to translate studies that were not published in English. However, we provide an R Shiny app (https://mcaloon-ucd.shinyapps.io/shiny2/) which facilitates testing the sensitivity of our pooled estimate to the inclusion of a single new study. This analysis demonstrates that our pooled estimate is largely unaffected by new estimates. Trialling the inclusion of a new study that reports considerably different estimates of the incubation period has very little impact on the overall pooled estimate.
It is worth noting that the parameter values from our meta-analysis are somewhat higher than previously used in modelling studies. For example, Ferguson et al38 used a mean of 5.1 days for incubation period, citing two previous studies.29 37 Mean incubation period from our meta-analysis was 5.8. Tuite et al,39 on the other hand, used an incubation period of 5.0 days citing the study by Lauer et al.27 This figure (5.0 days) was the median incubation period reported from that study,27 which is much closer to the median estimate of 5.1 days from our meta-analysis.
It is reasonable to assume that the incubation period estimated here should be relatively generalisable across different populations: unlike parameters such as serial interval, for example, incubation period depends only on the interaction between the virus and the host, which is expected to be similar across populations, and not on behavioural factors such as frequency of contacts which might be expected to vary across different countries. However, there is potential for a number of biases in these data which may impact on their external validity: in order to accurately estimate incubation period, it is possible that well-characterised cases may be preferentially chosen to reduce the impact of prolonged exposure windows. It is possible that such cases could be biased towards more severe cases. In that case, the estimate for incubation period could be biased downwards, since it is possible that the incubation period could be shorter in more severely affected individuals. Furthermore, these well-characterised cases (ie, those cases where exposure windows and dates of symptom onset are determined with a high degree of certainty) may not have been representative of all cases (often male, often younger34), highlighting the need for information on incubation period from older people, people with comorbidities, from women and those with mild symptoms. These findings are mostly based on studies from Chinese patients. While the incubation period for a given set of circumstances should be similar across different populations, there may be factors that might impact on incubation period, such as infectious dose, for example, that might vary between populations (and possibly within populations over the course of the outbreak), meaning that the resulting distribution may vary for different populations, or potentially at different stages of the outbreak. Incubation periods may also be different for people of different ages.13 Finally, a recent study has also suggested that patients undergoing surgery during the incubation period may have an accelerated progression to clinical signs, suggesting that those experiencing severe stresses during the incubation period may have a shorter time to the onset of clinical signs.40
Based on available evidence, we find that the incubation period distribution may be modelled with a lognormal distribution with pooled mu and sigma parameters of 1.63 (1.51, 1.75) and 0.50 (0.45, 0.55), respectively. It should be noted that uncertainty increases towards the tail of the distribution (figure 4 and table 2). The choice of which parameter values are adopted will depend on how the information is used, the associated risks and the perceived consequences of decisions to be taken. The corresponding mean was 5.8 days and the median was 5.1 days. These recommendations will need to be revisited once further relevant information becomes available. Accordingly, we present an R Shiny app which facilitates users to update these estimates as new data become available, https://mcaloon-ucd.shinyapps.io/shiny2/
E-mail:
Tel: +44 (0) 141 946 6482
Address: Healthcare Skills Training International Ltd
West of Scotland Science Park
Block 7, Kelvin Campus
Glasgow G20 0SP